Multimode Antenna Design Based on Symmetry Analysis of Characteristic Modes

This is due to the fact that the characteristic far fields are orthogonal to each other, offering pattern and polarization diversity. Therefore, the design of multimode antennas aims at exciting different sets of characteristic modes with different antenna ports in order to realize uncorrelated antenna ports, which are required for good MIMO performance.

However, the Theory of Characteristic Modes does not guarantee that the characteristic surface current densities themselves are orthogonal to each other. Instead, they may be correlated and can thus not be excited separately [1]. Antenna ports which excite overlapping sets of characteristic modes will be correlated [3] and thus do not offer optimal MIMO performance.

Regarding the orthogonality of the characteristic surface current densities, the symmetry of the antenna plays the decisive role [3]. This is due to the fact that the characteristic surface current densities are basis functions of the irreducible representations of the symmetry group of the antenna. For such basis functions, a fundamental orthogonality theorem from group theory exists, which states that those characteristic surface current densities that belong to different irreducible representations and those that form a degenerate set of the same multi-dimensional irreducible representation are orthogonal to each other. The orthogonality of the characteristic surface current densities is thus dictated by the symmetry of the antenna.

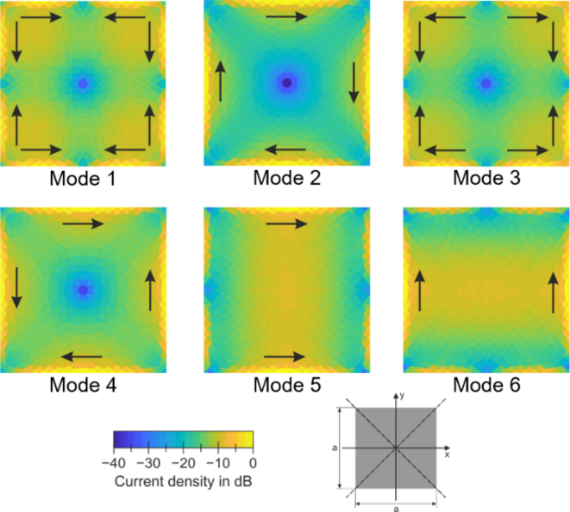
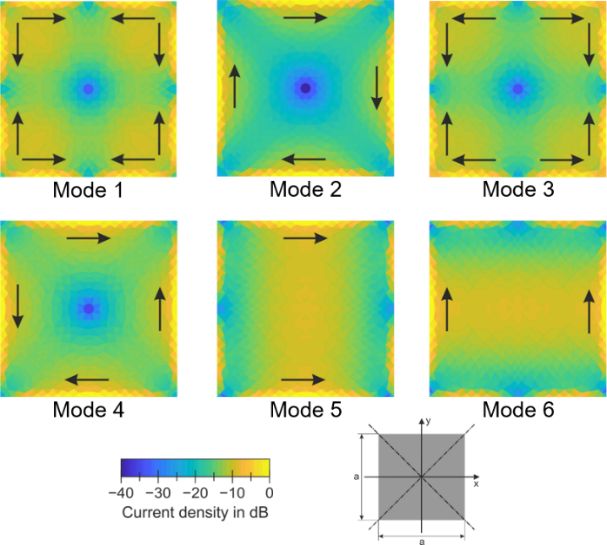
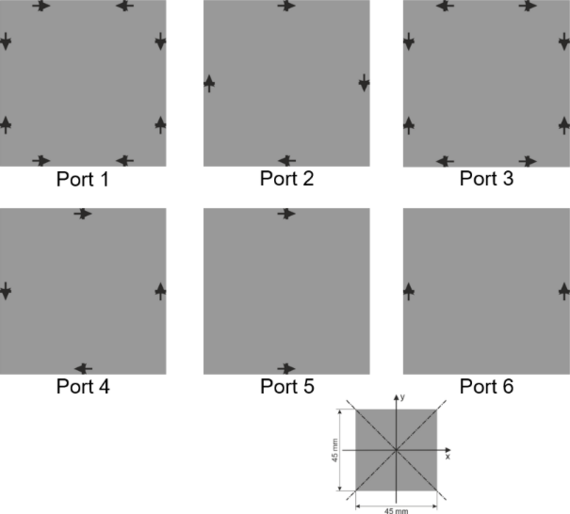
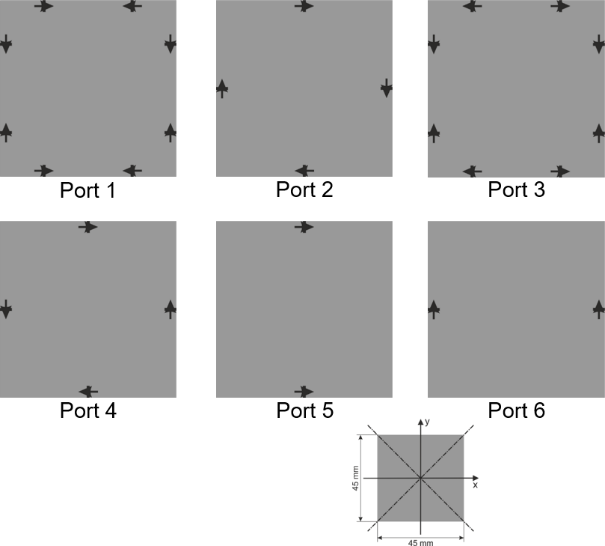
Fig. 1. Square plate with 45 mm edge length at 6 GHz. © 2019 IEEE [4]

A square plate as shown in Fig. 1 offers six mutually orthogonal sets of characteristic surface current densities because its symmetry group has four one-dimensional and one two-dimensional irreducible representations [3]. Fig. 1(a) shows for each set the surface current density of that characteristic mode which first becomes significant over frequency (fundamental modes). The surface current densities of higher order modes will each be correlated to one of these fundamental modes and thus do not provide any additional degree of freedom. Accordingly, the antenna size can be minimized such that only these six modes are significant at the operating frequency.

Another consequence of the orthogonality theorem is that an antenna port must have the same symmetry properties as the set of characteristic surface current densities it is intended to excite. A suitable port configuration for the square plate is shown in Fig. 1(b), where the antenna ports consist of symmetrically placed feed points whose relative phases are set in such a way that the symmetry requirements are fulfilled. This way, it is guaranteed that the ports only excite the characteristic modes of the corresponding set and are thus orthogonal to each other. At this point, it is noted that the number of orthogonal antenna ports is limited by the symmetry of the antenna. In other words, there is an upper bound for orthogonal antenna ports [3]. As another example, a regular hexagonal plate offers eight orthogonal antenna ports due to its higher symmetry [2].

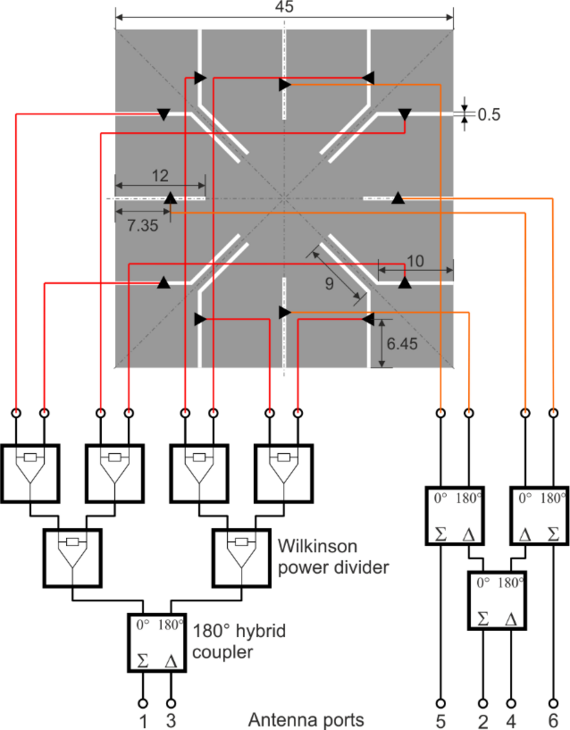
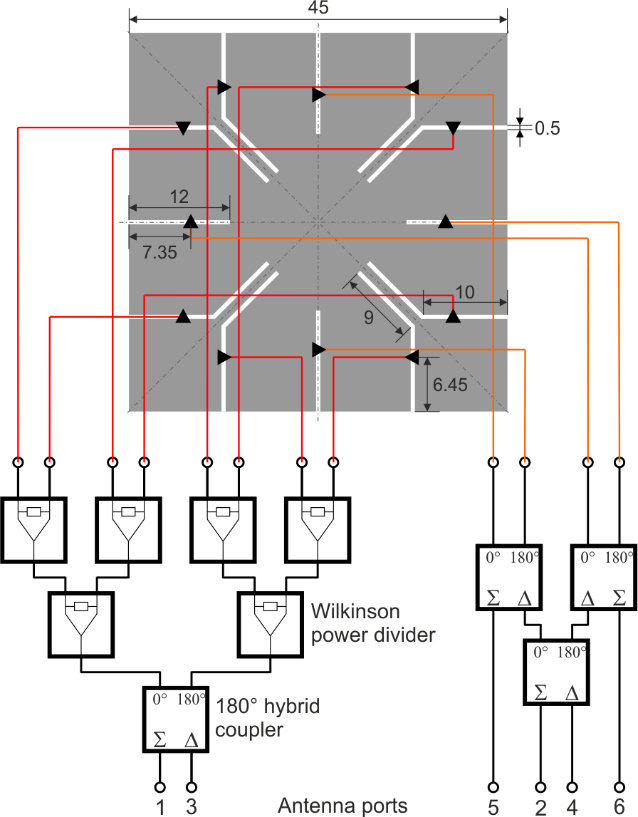
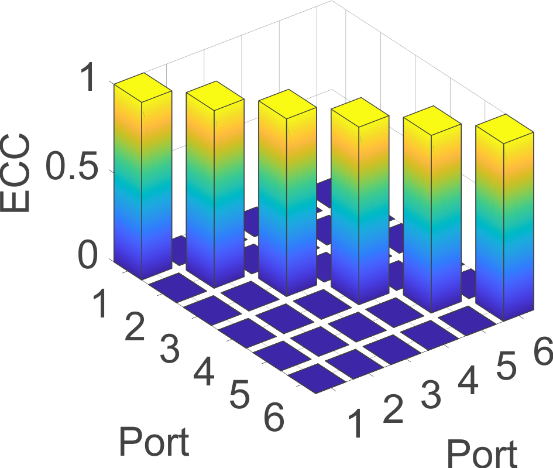
Fig. 2. Six-port multimode antenna based on square plate with excitation slots and feed network. © 2019 IEEE [4]

The idealized feed points in Fig. 1(b) are now replaced by practical excitation slots as shown in Fig. 2(a). By properly choosing the slot lengths and the positions of the feed points within the slots, the input impedances of the antenna ports can be adjusted. It is important that the symmetry of the square plate must not be altered by introducing the slots in order to preserve the orthogonality of the antenna ports. The orthogonality of the ports is confirmed by evaluating the envelope correlation coefficients (ECC) in Fig. 2(b).  Additionally, a feed network consisting of Wilkinson power dividers and 180° hybrid couplers is necessary in order to distribute the input signals to the feed points with the correct amplitude and phase relations [4].

The design of multimode antennas exploiting the symmetry properties of characteristic modes offers a systematic design procedure of multi-port antennas for MIMO applications. It is possible to determine how many orthogonal antenna ports can be realized on a given geometry or what antenna geometry should be chosen in order to realize a given number of antenna ports. Furthermore, instructions on how to realize the antenna ports and the feed networks can be derived.

[1] N. Peitzmeier and D. Manteuffel, "Selective excitation of characteristic modes on an electrically large antenna for MIMO applications," 12th European Conference on Antennas and Propagation (EuCAP 2018), London, 2018, pp. 1-5, doi: 10.1049/cp.2018.0779.

[2] N. Peitzmeier and D. Manteuffel, "Multi-Mode Antenna Concept based on Symmetry Analysis of Characteristic Modes," 2019 13th European Conference on Antennas and Propagation (EuCAP), Krakow, Poland, 2019, pp. 1-5.

[3] N. Peitzmeier and D. Manteuffel, "Upper Bounds and Design Guidelines for Realizing Uncorrelated Ports on Multimode Antennas Based on Symmetry Analysis of Characteristic Modes," in IEEE Transactions on Antennas and Propagation, vol. 67, no. 6, pp. 3902-3914, June 2019, doi: 10.1109/TAP.2019.2905718.

[4] N. Peitzmeier and D. Manteuffel, "Systematic Design of an Ultra-Wideband Six-Port Multi-Mode Antenna Element Using Symmetry Properties of Characteristic Modes," 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 2019, pp. 0466-0471, doi: 10.1109/ICEAA.2019.8878988.

[5] N.Peitzmeier and D. Manteuffel, "Systematic Design Method for Asymmetric Multiport Antennas Based on Characteristic Modes," 2020 14th European Conference on Antennas and Propagation (EuCAP), Copenhagen, Denmark, 2020.

[6] N. Peitzmeier, T. Hahn and D. Manteuffel, "Systematic Design of Multimode Antennas for MIMO Applications by Leveraging Symmetry," in IEEE Transactions on Antennas and Propagation, doi: 10.1109/TAP.2021.3098610.