Eigenvalue Tracking
Eigenvalue tracking [1] is one of the most important problems still not completely solved in the computation of characteristic modes. In general, the impedance matrix of the antenna structure varies over frequency. Therefore, the characteristic modes are frequency dependent as well. Since the characteristic mode computation is based on the Method of Moments, the modes are calculated for each frequency separately. The task of eigenvalue tracking is to trace the eigenvalues calculated at different frequencies over the whole frequency band of interest.
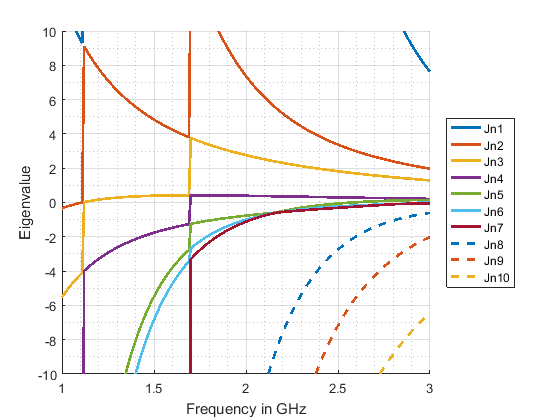


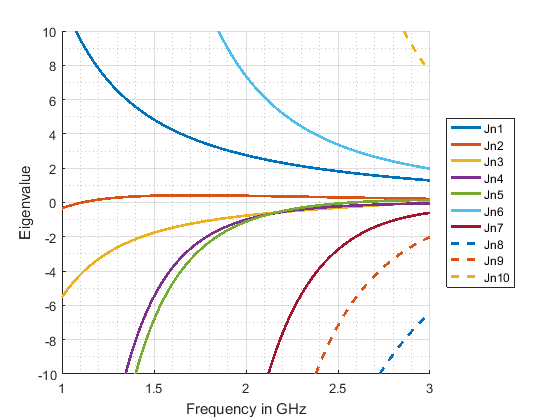


Figure 1 shows the eigenvalues of a rectangular PEC plate with dimensions 120 mm x 60 mm calculated with our in-house software CMC. In Fig. 1a, the raw eigenvalues are plotted as they are calculated at each frequency step. Applying a tracking algorithm to these unsorted eigenvalues (included in CMC) yields the plausible eigenvalue curves as shown in Fig. 1b.
However, there are cases where the tracking may fail. For instance, if two modes have the same eigenvalue at a given frequency (degenerate modes), a tracking error may occur, depending among other parameters on the frequency spacing and the chosen tracking algorithm. That is why there is still demand for further research and more sophisticated tracking algorithms.
Source Reconstruction Method
The source reconstruction method [2] is motivated by the fact that commercial software tools like Empire XPU are usually used for antenna design, but since an impedance matrix is generally not available in such tools (e.g. Empire XPU uses the finite-difference time-domain (FDTD) method), the characteristic modes cannot be calculated from the simulation models. In order to overcome this drawback, the source reconstruction technique was developed.
The basic idea is to compare the radiated far field of the complete simulation model with the characteristic far fields of a simplified model whose characteristic modes can be calculated with the Method of Moments. It is assumed that the simplified model has the same characteristic modes as the complete model. By correlating the total radiated far field of the complete model and the far fields of the characteristic modes, the modal weighting coefficients can be reconstructed, yielding the significant characteristic modes of the complete model.
Reactive Loading
Reactive Loading [3] is a technique that concerns the manipulation of the characteristic modes. If for example a given antenna structure has a suitable characteristic mode which is, however, resonant at the wrong frequency, how can the structure be manipulated in order to shift the mode to the desired resonant frequency? One possible solution to this problem without changing the structure’s geometry is the loading of the structure with lumped reactive loads.
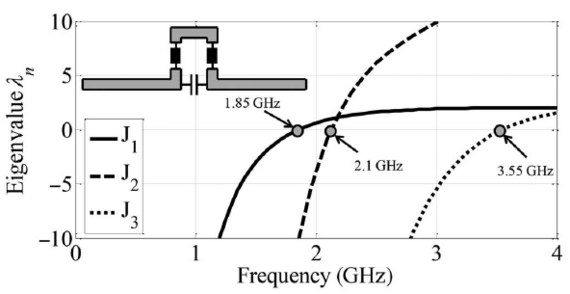


Such loading has a direct impact on the Method of Moments impedance matrix and thus changes the characteristic modes. If placed properly, the lumped elements may affect only certain modes while others remain unimpaired.
References
[1] E. Safin and D. Manteuffel, "Advanced Eigenvalue Tracking of Characteristic Modes," in IEEE Transactions on Antennas and Propagation, vol. 64, no. 7, pp. 2628-2636, July 2016, doi: 10.1109/TAP.2016.2556698.
[2] E. Safin and D. Manteuffel, "Reconstruction of the Characteristic Modes on an Antenna Based on the Radiated Far Field," in IEEE Transactions on Antennas and Propagation, vol. 61, no. 6, pp. 2964-2971, June 2013, doi: 10.1109/TAP.2013.2251312.
[3] E. Safin and D. Manteuffel, "Manipulation of Characteristic Wave Modes by Impedance Loading," in IEEE Transactions on Antennas and Propagation, vol. 63, no. 4, pp. 1756-1764, April 2015, doi: 10.1109/TAP.2015.2401586.